一、平均收益率
在某项证券投资跨越多个期间(如月份、年份等)的情况下,都需要进行平均收益率的计算。在投资实践中,衡量平均收益率最经常使用的是以下两个指标:
1.算术平均收益率
这是最简单的方法,即算术平均收益率(R)是将各单个期间的收益率(R)加总,然后除以期间数(n),计算公式如下:

算术平均收益率还假定,投资者通过追加或提取资金的方法始终将最初的投资金额保持不变。值得指出的是:当各期收益出现巨大波动时,算术平均收益率会呈明显的上偏倾向。算术平均数法适用于各期收益率差别不大的倩况,如果各期收益率差别很大的话,这样计算出来的收益率会歪曲投资的结果。
例如,某种股票的市场价格在第1年年初时为100元,到了年底股票价格上涨至200元,但时隔1年,在第2年年末它又跌回到了100元。假定这期间公司没有派发过股息,这样,第1年的投资收益率为100%(R1=(200-100)/100=1=100%),第2年的投资收益率则为-50%(R2=(100-200)/200=-0.5=-50%)。用算术平均收益率来计算,这两年的平均收益率为25%,即:R=[100%+(-50%)]/2=25%。而实际上,在整个投资期间,投资者并未赚到任何净收益。
2. 几何平均收益率
几何平均收益率使用了复利的思想,即考虑了资金的时间价值,也就是说,期初投资1元,第一期末则值(1+R1)元,第二期投资者会将(1+ 进行再投资,到第二期末价值则为(1+R1) (1+R2) 元,……。这个平均收益指标优于算术平均收益率,因为它引入了复利的程式,即通过对时间进行加权来衡量最初投资价值的复合增值率,从而克服了算术平均收益率有时会出现的上偏倾向。几何收益率(RG)的计算公式为:
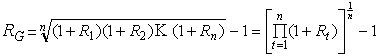
几何平均收益率的计算有个假定,即投资期间所获得的所有现金收益(如以现金形式派发的股息或红利等)都用于再投资。另外,它在计算过程中采用了即1加上收益率或用1减去亏损率的方法,进行如此技术处理的目的是为了避免几何平均数的计算因负的收益率的出现而变得毫无意义。
仍续上例,实际上,投资者尽管进行了两年的股票投资,但他的实际财富情况并未发生任何变化,其净收益为零。采用几何平均收益率来计算,RG=(1+1)(1-0.5)^1/2-1=0。这个计算结果符合实际情况,即两年来平均收益率为零。
算术平均数的上偏倾向使得它总是高于几何平均收益,而且收益波动的幅度越是大,这种偏差就越是明显。我们也可反过来说,假如算术平均收益与几何平均收益之间出现了较大差异,这说明市场上的投资收益波动非常剧烈。只有在整个投资期间各期的收益率都是相同的情况下,两种平均收益率才可能是一致的。
二、时间加权收益率
时间加权收益率是一种类似于几何平均收益率,考虑了资金的时间价值,运用了复利思想的收益率。它与几何平均收益率的区别在于:时间加权收益率不开n次方,而几何平均收益率则要开n次方。这意味着,时间加权收益率说明的是1元投资在n期内所获得的总收益率,而几何平均收益率是计算1元投资在n期内的平均收益率。时间加权收益率(RTW)的计算公式为:
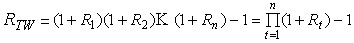
三、实际收益率
投资者投资于某种有价证券,实际上是放弃了当前消费,因而他们就应该得到相应的补偿,即将来得到的货币总量的实际购买力要比当前投入的货币的实际购买力有所增加。在不存在任何通货膨胀和其他投资风险的情况下,这个增量就是投资者的实际收益率,也就是货币的时间价值。但是,假若投资者预期价格在投资期内会上涨,即存在通货膨胀,那么投资者就必须考虑通货膨胀对货币购买力的影响。投资于某证券的实际收益率(Rreal)等于名义收益率(Rnom)扣除通货膨胀率(h)的收益率:
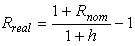
从实际收益率公式可以看出它的两条性质:第一,如果通货膨胀率为零,实际收益率便等于名义收益率;第二,如果名义收益率与通货膨胀率相等,实际收益率便等于零。
实际收益率还可以近似地写成名义收益率减去通货膨胀率:
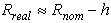
这是由美国经济学家欧文·费雪(Irving Fisher,1867-1947)提出的著名的费雪关系式。
此外,我们还可以运用几何平均法计算若干时期的实际平均收益率,可称之为实际几何平均收益率(Rreal.g),其计算公式为:
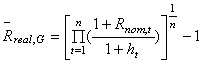
对比上述几何平均收益率可见,那里的几何平均法计收益率其实是名义几何平均收益率。
四、期望收益率
证券投资收益往往具有较大的不确定性,可以用证券投资的期望收益率这一指标来加以度量。证券投资的期望收益率就是证券投资的各种可能收益率的加权平均数,以各种可能收益率发生的概率为权数。采用这一计算方法的基本前提是,投资者能够描述出影响收益的各种可能情况,各种情况出现的概率及收益的大小。其计算公式如下:
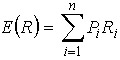
其中,E(R)表示期望收益率;Pi表示出现第i种情况的概率,o<Pi<1,∑Pi=1;Ri表示第i种情况下的收益率。